Primer expliqué

Il y a quelques semaines j’ai eu l’occasion de découvrir Upstream Color, le dernier (deuxième) film de Shane Carruth. Je ne parlerai pas de ce film qui est une œuvre cinématographique unique, complexe, envoutante, déconstruite, et qui demande plusieurs visionnages pour tenter d’en éclaircir le sens. Difficile à résumer, donc faites-en votre propre avis, en vous procurant le film par vos propres moyens vu que la date de sortie en salle en France n’est pas encore annoncée (Yarr!).

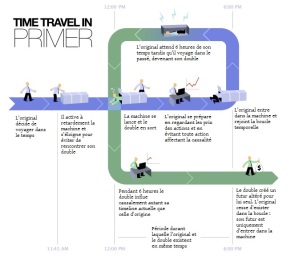
Mais ça m’a donné l’occasion de revoir une fois encore Primer, le premier film de Shane Carruth. Primer est un film extrêmement complexe par sa narration concise, et vous mentira celui qui vous affirmera l’avoir parfaitement compris en un seul visionnage (après 10 fois certains passages m’échappent encore). Cette fois-ci les personnes l’ayant vu avec moi n’ayant “rien compris à ce truc”, pourquoi ne pas essayer sur ce blog d’en démêler l’histoire ?

Primer est un film qui traite du voyage dans le temps, qui est probablement mon sujet de fiction favori. Mais les voyages dans le temps, c’est compliqué (et c’est ce qui font leur intérêt narratif) et surtout impossible, il faut ainsi poser des bases solides sur les contraintes et les règles physiques qui régissent le monde – fictif – dans lequel on se trouve. Retour vers le Futur (de loin mon film préféré en la matière) le fait brillamment et ludiquement en utilisant le personnage de Marty, un jeune de 17 ans, se faisant expliquer, et le spectateur par la même occasion, par le Doc toutes les conditions qu’implique le voyage dans le temps. Dans Primer on assiste à des discussions entre deux « Doc », deux ingénieurs immensément doués, qui ne prennent pas la peine d’expliquer le b.a.-ba de la physique et ne font aucun effort pour paraître clair au spectateur, qui devra apprendre à décoder les bouts de dialogues désordonnés que le film voudra bien nous servir.

Il est remarquable de noter que le film a été réalisé avec un budget de 7000$. Cela se voit évidemment dans le rendu d’image et de son (les caméras HD n’étaient pas courantes à l’époque), et se ressent dans la mise en scène. N’ayant pas la possibilité d’apparaître à l’écran en même temps que son double, le réalisateur et acteur Shane Carruth a du jouer d’ingéniosité pour contourner cette limitation. Même si vous êtes totalement bilingue, je conseille de le regarder avec les sous-titres, une partie des dialogues étant difficiles à comprendre voire quasiment inaudibles.

Le voyage dans le temps.

Avant de se lancer dans le vif de l’histoire, voyons d’abord rapidement comment fonctionne leur machine à voyager dans le temps dans ce film.
Lorsque la machine est activée, une sorte de « chaîne » dans l’espace-temps se créé, un champ magnétique va progressivement se construire, à partir du point A, disons à 12h00, mettant plusieurs secondes ou minutes, selon la taille de la machine, pour se stabiliser.
Quand la machine est éteinte, le champ se réduit jusqu’à zéro, fermant la chaîne au point B, disons à 12h01.
Un objet placé dans la chaîne, c’est à dire à l’intérieur de la boîte et temporellement entre les points A et B, ne va pas se déplacer dans le temps de façon naturelle, parce que le temps ne circule pas à l’intérieur de la chaîne comme dans la réalité. Cet objet va errer du point A au point B, d’avant en arrière, de façon répétée, dans un état indéterminé, le temps s’accumulant de son point de vue seulement.
Cela continue jusqu’à ce que l’objet soit retiré de la machine, au point A ou au point B. A chaque fois que le l’objet atteint une extrémité de la chaîne, il y a une faible probabilité qu’il en sorte au lieu de continuer un trajet dans l’autre direction. Pour une raison inexpliquée il apparaît que c’est au bout d’environ 1300 parcours A-B que les chances font que l’objet en sorte, de façon à ce que pour l’objet, le temps passé à l’intérieur de la chaîne est variable mais toujours autour de 1300 minutes.
Si l’objet est placé au point A, au moment où la machine est allumée, d’un point de vue extérieur il ne peut en sortir qu’au point B, et fait donc un nombre impair de trajets entre A et B. Dans l’expérience du film, ils observent un temps de 1347 minutes.
Si l’objet est placé au point B, à l’arrêt de la machine, il ne peut sortir qu’au point B après un nombre pair de trajets. Ils trouvent ainsi dans le film un temps de 1334 minutes.
Ces expériences concernent des objets inanimés, qui ne peuvent choisir le moment où ils sortent de la machine. Un objet placé en B ne peut sortir qu’en B puisque c’est ainsi qu’ils le voient à la fin de leur expérience. Mais un robot par exemple, entré au point B et programmé pour mesurer le temps écoulé dans la machine, pourrait sortir de lui-même de la machine au point A et ainsi voyager dans le passé. Aaron et Abe sautent cette étape et envisagent directement de voyager dans le temps eux-mêmes.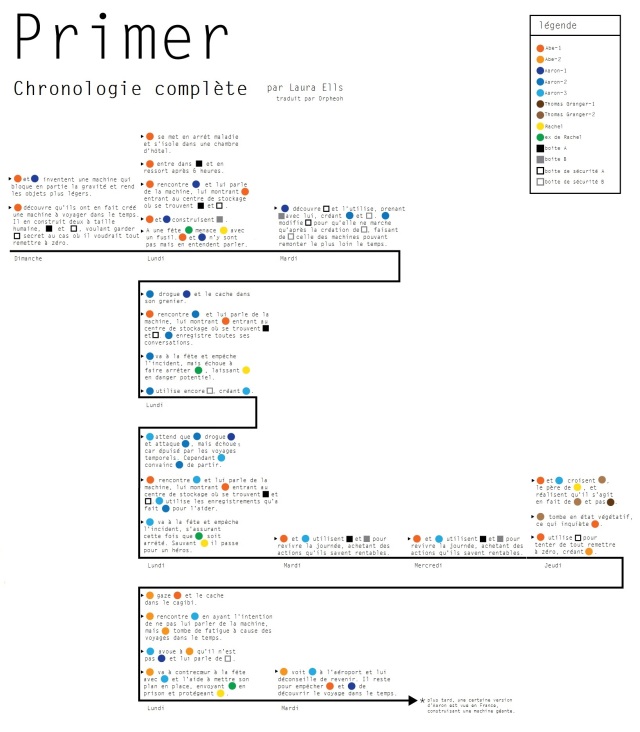

Résumé

Aaron et Abe au premier plan, Robert et Philip à l’arrière.

Aaron, Abe, Philip et Robert sont quatre ingénieurs qui occupent leur temps libre en vendant de l’électronique. Malgré quelques brevets ça ne suffit pas à leur rapporter assez d’argent (il est également sous-entendu qu’un certain Platts leur a volé un de leurs brevets).
Dans le garage d’Aaron ils construisent (en utilisant divers équipements, des pièces du réfrigérateur neuf – la scène se passe peu après Noël – d’autres qui seront prises depuis leur lieu de travail) une boîte qui se révèle avoir la propriété de réduire la masse des objets placés à l’intérieur. Aaron et Abe se rendent compte après qu’une partie du design de Philip et Robert est superflue et que la machine semble marcher parfaitement. En manipulant l’appareil Aaron et Abe placent tous deux leurs mains au-dessus du champ généré, ce qui aura de l’importance par la suite.

La boîte est scellée hermétiquement et la caméra à l’intérieur leur renvoie un signal brouillé parce que le contenu de la boîte est indéterminé. Ils la remplissent d’argon, y placent un Weeble à l’intérieur, constate une réduction de sa masse. La machine tombe ensuite en panne de façon inexpliquée.
Un peu plus tard, Aaron a modifié et réparé la machine. Il constate même trouver plus de courant en sortie qu’en entrée, et s’étonne qu’elle continue à fonctionner quelques minutes après que le courant soit coupé. Abe et Aaron réalisent très vite les nombreuses applications possibles qu’ils pourraient en tirer et décident de ne pas en parler à Robert et Philip, prétextant une désinfection du garage.
Quelques mois plus tard, ils sont financés par Thomas Granger. Abe sort par ailleurs avec la fille de ce dernier, Rachel, tandis qu’Aaron a une femme Kara et une fille Lauren. Durant tout ce temps Abe essaie en vain de comprendre le fonctionnement de la machine.
Tout s’accélère. Après de nombreuses expériences avec le Weeble, Abe constate qu’une sorte de champignon a poussé dessus. Des analyses révèlent que ce type de champignon est tout à fait ordinaire, mais qu’une telle quantité ne s’obtient que sur des années et pas en quelques jours. Plaçant une montre à l’intérieur, il conclut que leur dispositif est une machine à voyager dans le temps.
Abe réussit à construire une machine à taille humaine, que nous appellerons Boîte A, qu’il cache dans un centre de self-stockage.

Nous sommes maintenant au mois de mars, un lundi.

Lundi

A 8h30, Abe programme la boîte A pour qu’elle s’active d’elle-même 15min après. Il quitte le centre de stockage en voiture et s’isole dans un hôtel à Russellfield. La boîte s’active à 8h45 et est complètement chargée à 8h49.
A 15h15, Abe retourne éteindre la boîte A, qui met 4 minutes à s’éteindre complètement. Pendant qu’elle s’éteint il grimpe à l’intérieur, attend pendant six heures (six heures et demi en fait contrairement à ce qui est dit dans le film). Il en ressort au bon moment, juste après que la boîte ait été activée, à 8h45. Tandis que son “double” est enfermé à l’hôtel, il va voir Aaron, qui sur son banc, écoute March Madness (un championnat de basketball) sur ses écouteurs (qu’il gardera tout au long de la journée).
Abe montre à Aaron tous les éléments qui l’ont amené à conclure que leur machine pouvait servir à voyager dans le temps – les champignons et la montre, puis à 15h15 il amène Aaron devant le centre de stockage où ils voient le double d’Abe entrer dans le boxe et disparaître. Aaron est désormais convaincu.

Mardi

Abe va répéter pas à pas ses actions de la veille, rejoint par Aaron qui a entre-temps fait construire sa propre machine. Ils allument les boîtes A et B à 8h30, se cachant à l’hôtel toute la journée, et y retournent à 15h15. Abe ressort de la boîte comme prévu à 8h45 mais Aaron en sort une minute trop tôt (ou trop tard du point de vue d’Abe) et en subit des effets secondaires.
Ils s’isolent à l’hôtel pour éviter de provoquer des paradoxes, en particulier tout ce qui pourrait amener leurs doubles à ne pas rentrer dans les boîtes comme prévu, ce qui aurait entrainerait la présence de leurs doubles de façon permanente. Une passage important des dialogue mentionne qu’ils croient que les boîtes sont à usage unique. Aaron veut ainsi dire qu’après être sorti de la boîte il n’est pas possible d’y retourner plus tard, de l’éteindre et d’y rentrer une seconde fois, parce que c’est déjà ce que son soi-passé a fait. Il est impossible de revivre le même jour dans une boucle infinie en utilisant la même boîte.
Ils gagnent de l’argent en vendant des actions et le soir, légèrement éméchés, ont une conversation avec Kara, la femme d’Aaron sur la perspective d’être infiniment riche. Aaron évoque le fait de pouvoir frapper Joseph Platts et de retourner en arrière comme pour annuler cet acte, Abe lui répond “we can’t do that”, non pas pour signaler que ce serait moralement mauvais de le frapper, ou parce qu’Aaron ne peut pas parler à Kara à propos de la machine, mais parce qu’à ce moment ils supposent tous deux que l’histoire ne peut être modifiée.
Au passage dans la discussion, Kara mentionne des bruits étranges dans leur grenier. Peut-être des rats ou des oiseaux…

Mercredi

Même routine que la veille. Ils ont une discussion au supermarché et à la station-service à propos des paradoxes temporels, du libre-arbitre, de l’incertitude sur le fait de vivre dans un univers modifié par quelqu’un d’autre. A l’hôtel puis à la bibliothèque, ils abordent le problème d’Aaron de ne pas parler des machines temporelles à sa femme, ainsi que de les garder secrètes de Robert et Philip, en leur cédant des brevets ou de l’équipement pour préserver leur bonne conscience.
Ils retournent en arrière comme prévu. A 8h15, peu après être sorti de la machine, Aaron a son oreille qui saigne. Ils effectuent leurs transactions et rentrent en fin d’après-midi au garage où ils avouent à Robert et Philip, avant de reprendre leur travail, que le garage a été encore désinfecté. Robert fait alors le récit d’une histoire intéressante. Lundi soir se déroulait la fête d’anniversaire de Robert. Abe n’y était pas, mais sa copine Rachel s’y trouvait, ainsi que l’ex de Rachel qui y a débarqué avec un fusil. Aaron qui était là également s’est alors interposé, risquant sa vie pour désamorcer la situation.
Durant la soirée (mercredi toujours), Aaron et Abe sont dehors à chercher le chat d’Aaron. Abe reproche à Aaron, père de famille pourtant, d’avoir pris de tels risques lors de la fête, et ne comprend pas comment il a pu agir aussi inconsciemment. Aaron essaie de se justifier en expliquant que depuis la découverte de la machine temporelle il voit le monde différemment, faisant référence aux discussions de la matinée. Mais ça ne suffit pas à expliquer son acte.

Jeudi

Même routine encore.
Alors qu’ils passent la journée à attendre à l’hôtel, le téléphone portable d’Aaron se met à sonner. C’est sa femme Kara, lui parlant du diner. Aaron fait l’erreur de décrocher, alors qu’ils sont censés s’isoler. Abe demande à Aaron de ne pas emporter son téléphone portable dans la machine, pour éviter les paradoxes.
Ils retourne en arrière, comme à leur habitude. A l’hôtel, Aaron regarde un match dont il connait déjà le résultat et Abe mange un muffin.
En chemin vers un restaurant le téléphone d’Aaron, qu’il a malencontreusement oublié avec lui se (re)met à sonner. C’est un problème et un point critique du film. Il y a deux Aaron en même temps, dont le premier à l’hôtel, et à cause de l’erreur d’Aaron, deux téléphones portables, dont un à l’hôtel. Si le téléphone dans la main d’Aaron sonne, et si le raisonnement d’Abe et Aaron est correct (le réseau scannant chaque zone et sonnant le premier téléphone qu’il trouve), alors le téléphone de l’hôtel ne peut pas sonner. La symétrie a été brisée et prouve que l’histoire peut être changée.

Vendredi

A 2h du matin Abe est réveillé par des jeunes qui s’amusent à déclencher les alarmes de voiture.
Abe va chez Aaron et le réveille. Il lui révèle qu’il a pris l’habitude d’allumer les machines tous les soirs à 17h et de les éteindre le matin suivant. Abe explique ensuite un plan potentiellement dangereux, consistant à aller chez Joseph Platts, et de le frapper, puis, vers 3h du matin, d’utiliser les boîtes pour remonter le temps jusqu’à jeudi 17h et de faire en sorte que ni les alarmes ni l’agression sur Platts ne se produisent. Le résultat théorique étant que les doubles d’Abe et Aaron n’auraient aucune raison de se réveiller en pleine nuit, et ce vendredi ils iraient comme d’habitude dans leur boîte à 15h15, quittant définitivement cette timeline et ne laissant qu’une seule version d’Abe et Aaron.
Ce plan fonctionnerait-il ? Bonne question.
Cependant en montant en voiture ils se rendent compte qu’ils sont suivis par Thomas Granger, le père de la copine d’Abe et leur principal financeur. Granger a alors une barbe de 2-3 jours, alors qu’Aaron affirme l’avoir vu parfaitement rasé ce jeudi même. Abe appelle le téléphone de Granger qui répond lui-même, mais ce n’est pas le Thomas Granger qui les suit alors ! Cet homme est un autre Thomas Granger qui est revenu dans le temps en utilisant une des boîtes, probablement sortant jeudi à 17h quand Abe l’a allumée. Aaron part à la poursuite de Granger et alors qu’il s’approche de lui trébuche tandis que Granger tombe totalement inconscient. Ils cachent Granger chez Abe ; il se trouve qu’Aaron ne peut pas s’approcher de lui sans le rendre inconscient.
Ils vérifient que les boîtes sont effectivement allumées, Aaron propose de les éteindre pour voir si Granger est bien à l’intérieur mais ils ne le font pas. Il est difficile d’imaginer ce qui ce serait alors produit.

Pourquoi Granger était-il revenu dans le passé ? Il est évident qu’à un certain moment dans le futur, Abe ou Aaron auront parlé des machines à Granger. Quelque chose aurait ensuite poussé Granger à revenir ce point dans le temps (le plus loin qu’il puisse remonter). Ils concluent que la situation a du être une vraie urgence mais n’ont aucune idée de ce que ça peut être. Le cours de l’histoire a été changé maintenant que Granger est revenu, mais ils ne savent pas si l’urgence en question a été justement résolue, Granger n’ayant été hors de la machine que pendant huit heures trente.

Il est maintenant révélé que Abe avait construit une machine de sécurité dans un autre centre de stockage. Cette machine est allumée depuis 3 jours et 22 heures, c’est à dire depuis lundi matin. Abe a lancée cette machine à 5h du matin lundi, est allé se recoucher jusqu’à 8h30 pour ensuite allumer la boîte A. A environ 3h du matin vendredi, Abe se rend à cette machine de sécurité, avec quatre jours d’oxygène, de l’eau et du protoxyde d’azote, y entre et voyage dans le temps jusqu’à lundi.

Lundi, encore

Abe-2 sort de la machine de sécurité à 5h et gaze son double avec le protoxyde d’azote avant de l’enfermer dans la salle de bain.
On retourne à la scène du banc. Comme durant la première scène, Aaron écoute ce qu’on croit être du basketball, Abe-2 se sent mal, après quatre jours sans manger et le choc d’avoir gazé son double. Aaron pourtant répète les mêmes dialogues que la première fois.
En fait, quand Abe s’évanouit, il est révélé qu’Aaron n’écoute pas du basketball mais les enregistrements exacts de cette conversation. Comment serait-ce possible ? Ce n’est pas l’Aaron d’origine. Ce n’est pas la timeline d’origine et ne l’a jamais été. Cet Aaron est revenu du futur.
Abe et Aaron s’expliquent tout ce qui vient de se passer. Arrive la séquence la plus difficile à suivre du film, due à la complexité du récit et en partie à cause du manque d’effets spéciaux empêchant de montrer plusieurs Aaron à l’écran.

Comment Aaron est-il revenu ?
“They are not one-time use only.. They are recyclable” Aaron explique que bien qu’on ne puisse pas ré-entrer dans une boîte d’où on vient de sortir, on peut y amener une boîte avec soi, l’activant une fois sorti pour l’utiliser plus tard et revenir au même instant encore (ou avec juste quelques minutes de décalage).
Dans une timeline précédente, Aaron a découvert la machine de sécurité d’Abe. Il est monté dedans en prenant avec lui une seconde machine repliée qu’il reconstruira ensuite. C’est le Aaron qu’on voit avec une capuche.
Lundi aux alentours de 5h15, le Aaron à capuche (Aaron-2) allume sa deuxième boîte, une machine de sécurité B. Il se rend ensuite chez lui et drogue le lait de son double, puis va cacher son double inconscient dans le grenier. Ce sont les bruits mentionnés par Kara le mercredi soir. Ca veut dire qu’il y a maintenant et de façon définitive deux Aaron dans cette timeline. Aaron-2 prend la place de son double et se met à enregistrer toutes les conversations de la semaine.
Il utilise ensuite la machine de sécurité B (il ne peut pas monter dans la machine A qu’il a déjà utilisée) pour revenir au lundi 5h15, en prenant une fois encore une autre machine avec lui, qu’il activera en tant que machine de sécurité C (vers 5h30 lundi). Il devient Aaron-3, en pull blanc sans capuche. Il arrive chez lui juste quand Aaron-2 finit de droguer et de cacher le Aaron d’origine dans le grenier. Aaron-3 essaie à son tour de neutraliser Aaron-2, mais trop fatigué par les voyages dans le temps c’est Aaron-2 qui prend le dessus. Cependant après une conversation, Aaron convainc Aaron-2 de partir. Il y a maintenant trois versions permanentes d’Aaron : Aaron-‘Prime’, drogué dans le grenier, Aaron-2 qui a quitté la ville, et le troisième Aaron qui est celui qu’on a suivi à l’écran depuis la première scène du banc, avec ses écouteurs lui donnant tous ses dialogues.
Aaron-3 a passé beaucoup de temps dans les machines, c’est pourquoi il a commencé à saigner de l’oreille le mercredi et c’est aussi pourquoi son contact avec Thomas Granger a failli le tuer.
Le narrateur de l’histoire, au téléphone, est quant à lui Aaron-2.
Pour qu’Abe ait pu remonter dans le temps, il a du utiliser la machine de sécurité C, puisque la machine A contenait Aaron-2 et la machine B contenait Aaron-3. C’est donc qu’Aaron a échangé la machine A (démarrée à 5h) et C (démarrée à 5h30), le film ne mentionnant pas ce point.

Pourquoi Aaron est-il revenu ?
Dans quel but Aaron s’est-il impliqué autant, à remonter autant le temps, y sacrifiant sa santé et au point de se dupliquer deux fois ?
La clé de tout ça est la fête. Il est évident que lorsque l’ex de Rachel est apparu un fusil à la main, les choses auraient pu gravement dégénérer. On se souvient qu’Aaron-3 a risqué sa vie pour régler la situation. Il y a deux autres Aaron dans cette timeline, l’un étant celui d’origine. Ainsi Aaron n’a pas d’importance, il n’existe pas aux yeux de la société, sans droit sur la famille d’Aaron-Prime c’est un mort en sursie qui n’a donc pas de vie à risquer.
Un autre point du film est aussi important. Il apparait lors de la scène du basket (au milieu de lundi) que c’est Aaron lui-même qui a invité Will, le cousin de l’ex de Rachel, à la fête, et que c’est Aaron qui lui a suggéré d’y amener l’ex de Rachel avec lui. Ce qui s’est passé originellement à la fête est donc indirectement la faute d’Aaron qui se sent responsable et explique ce qu’il a fait pour y remédier.
Aaron-3 pensait avoir régler le problème. Mais le fait que Thomas Granger soit revenu dans le temps à 17h jeudi prouve que son action a été insuffisante et que quelque chose de grave se trame toujours dans futur d’Abe et d’Aaron. Abe-2 et Aaron-3, maintenant tous deux au courant des événements futurs (sachant qu’aucun coup de feu ne sera tiré “Okay? We’re prescient.”) peuvent mieux s’occuper de la situation (en s’assurant de retirer les balles) et envoyer l’ex de Rachel en prison.
Lundi après-midi, Aaron et Abe souffrent tous deux d’effets secondaires aux voyages dans le temps et ne sont plus capables d’écrire correctement (les mains dans la machine, remember?).
A ce moment le narrateur, Aaron-2 à la capuche, nous rappelle que lui ne vient pas d’une timeline où tout s’est bien déroulé. Aaron-2 n’est allé qu’une seule fois à la fête et n’a vu qu’une seule fois comment tout allait se passer. Il ne sait pas combien “d’essais” à revenir dans le temps ça prendra à Aaron-3 pour arriver à tout régler parfaitement (“So how many times did it take Aaron as he cycled throgh the same conversations lip-synching trivia over and over? How many times would it take before he got it right? Three? Four? Twenty?”).De ce qu’on voit dans le film, Abe-2 et Aaron-3 y arrivent du premier coup. L’ex jaloux est arrêté. Happy ending. Sauf que…

Mardi, encore

Aaron-Prime se réveille dans son grenier après avoir été drogué 24h par son double. Abe-Prime se réveille dans sa salle de bain après avoir été gazé 24h par son double. Il y a encore trois machines de sécurité qui sont en train de fonctionner, sans compter la boîte d’origine A d’Abe qui n’a pas encore été activée mais est néanmoins opérationnelle. “They’ll be building their own boxes in another day. And yours (Abe-Prime) already knows what they’ve built.”
Aaron-3 et Abe-2 se retrouvent à l’aéroport. Aaron-3, ayant volé le passeport de son double, prévoit de quitter le pays, car il ne peut plus jamais retourner chez lui. Il doit laisser sa femme et sa fille à Aaron-Prime. Abe, quant à lui, décide de rester pour saboter les tentatives de leurs doubles de construire des machines à voyager dans le temps (et pour surveiller Kara et Lauren et les protéger d’Aaron-3).
Enfin, à l’autre bout du monde, Aaron-2 appelle Aaron-Prime. Peut-être que ce dernier aura enregistré l’appel et le croira, peut-être que non. Aaron-2 explique toute l’histoire, y compris pourquoi il a drogué Aaron-Prime (“Now I have repaid any debt I may have owed you.”).

“You will not be contacted by me again. And if you look, you will not find me.”

Aaron-2 raccroche, et commence la construction d’une machine (d’une seule géante ou de plusieurs ?) dans un hangar. The End.

Ce serait trop réducteur de prétendre résumer intégralement ce film de la sorte, de nombreuses interprétations et analyses existent sur le net, principalement en anglais, bien plus détaillées que le maigre article présenté ici. Pour plus d’informations sur le film, je vous invite à consulter la cinquantaine d’articles de ce blog très complet.
Un grand merci également au blog de qntm.

Les prisonniers et l’ampoule [Solution]

Nos pauvres prisonniers peuvent-ils espérer s’en sortir (vivants si possible) ? L’énoncé du problème ne mentionnait pas leur espérance de vie, ainsi on ignorera la vraisemblabilité d’une réponse qui leur ferait pourtant attendre des centaines d’années (voire bien plus). Ici nos prisonniers sont immortels (sauf quand ils sont exécutés :p), ces chanceux !

Parlons déjà d’une solution qui n’en est pas une, qui est celle d’utiliser les probabilités.

Le gardien choisissant au hasard, de façon uniforme, nos prisonniers peuvent se dire qu’au bout d’un certain temps, les chances que chacun ait été appelé seront suffisamment élevées pour qu’ils puissent sans risque affirmer être tous passés dans la salle. Je tiens cependant à dire que l’énoncé précisant bien qu’il leur faudrait une certitude absolue pour s’en sortir, cette solution n’est pas valable pour notre problème. Il est tout à fait possible, mais avec une probabilité quasi-nulle, qu’un des prisonniers ne soit jamais pris sur une période de mille ans. Mais pour son intérêt mathématique, étudions-là de plus près.

On retrouve ici une version du problème du collectionneur de coupons, qui se pose ainsi : On suppose qu’il y a n coupons différents de probabilité égale à obtenir, et on regarde le nombre d’essais T qu’il faudra faire pour collecter l’ensemble des coupons. S’il est facile d’obtenir les premiers rapidement, les derniers demanderont un temps bien plus élevé (pour une collection de 42 coupons, il faut effectivement 42 essais en moyenne pour obtenir le dernier si l’on est déjà en possessions des 41 premiers). C’est pourquoi le temps moyen pour collecter l’ensemble est bien plus long que le nombre de coupons lui-même.
On trouve facilement que l’espérance de ce temps T se calcule ainsi :

On pourra calculer E(T) – ou s’en rapprocher via le développement asymptotique de Hn –  et trouver par exemple que pour 42 coupons, le temps moyen pour réunir l’ensemble des coupons est de 182 essais.

Retournons à nos prisonniers. Ils décident simplement d’attendre que la probabilité qu’ils aient été tous choisis soit suffisamment forte pour annoncer sans risque que c’est bien le cas. On pourra prendre une valeur arbitraire comme 99.9%.
Pour calculer la probabilité exacte qu’ils auraient d’être tous choisis après un temps T, on va utiliser une matrice stochastique (ou de Markov), la matrice M de taille 42×42 des transitions.

Très bien. On notera que la probabilité au bout de 2048 jours n’est pas exactement 1 contrairement à ce que mon tableur m’indiquera, mais plutôt 0.999… avec un certain nombre de 9.
Soit. Au bout de 1024 jours la probabilité qu’ils aient été tous choisis est supérieure à 99.9%, nos prisonniers pourraient donc s’estimer satisfaits de ces chances et l’annoncer au gardien. Mais ce n’est pas la solution attendue pour ce problème. Fin de notre digression.

Voyons d’abord une solution bien inefficace.
Les prisonniers répartissent les jours en blocs de 42 jours et chacun passant dans la salle  applique le procédé suivant :

• Si c’est le 1er jour du bloc :

– Si l’ampoule est éteinte, il l’allume.
– Si elle est déjà allumée, et que le premier bloc de 42 jours est déjà passé plus tôt, il annonce au gardien que tous les prisonniers sont passés dans la pièce.

• Pour tous les jours du bloc :

– Si c’est sa première visite dans la pièce durant ce bloc, il ne fait rien.
– Si c’est son second passage ou plus dans la pièce durant ce bloc, il éteint l’ampoule (ou la laisse éteinte si elle l’est déjà).

L’idée derrière cette stratégie est qu’éventuellement, avec une probabilité 1, les prisonniers seront assez chanceux pour qu’il y ait un bloc de 42 jours où aucun d’entre eux ne passera dans la pièce deux fois. C’est à dire que chacun n’y entrera qu’une et une seule fois. Ainsi l’ampoule sera allumée le premier jour et le restera après 42 jours, n’étant éteinte qu’en cas de deuxième passage. Au premier jour du bloc suivant, le prochain prisonnier saura donc qu’au bloc précédent chacun d’entre eux y est passé et pourra l’annoncer au gardien.
Bon il y a un petit problème cependant. Pour un bloc donné, la probabilité de succès est le nombre de permutations des 42 prisonniers divisé par le nombre de façon possible qu’ils aient d’entrer dans la pièce. Pour n prisonniers, c’est (n!/n^n).
Le nombre moyen de blocs pour y arriver est égal à 1/p où p est la probabilité de succès dans un bloc.  Ainsi le nombre moyen de blocs est de n^n/n!. Chaque bloc étant de n jours, le nombre moyen de jours avant leur libération est de n^(n+1)/n!.
Pour info, pour nos 42 prisonniers, ça fait quand même 4.48*10^18 jours, soit un peu plus de 12 millions de milliards d’années. Faut être patient.
Bon ils auraient plutôt intérêt à se mettre d’accord sur une méthode qui aboutisse avant la fin de l’univers.

Voici la solution classique à l’énigme :
Les prisonniers se mettent d’accord pour faire de l’un d’eux le Compteur. Grâce à une stratégie particulière, ce Compteur sera chargé de déterminer lorsque chacun de ses camarades sera passé dans la pièce et d’annoncer lui-même au gardien que tous y sont allés de façon sûre. Cette stratégie est la suivante. Quand un prisonnier, autre que le Compteur, entre dans la pièce :
– Si l’ampoule est éteinte et qu’il ne l’a jamais lui-même allumé, il l’allume.
– Si elle est déjà allumée ou s’il l’a déjà allumé lui-même, il ne fait rien.
Lorsque maintenant le Compteur entre dans la pièce :
– Si l’ampoule est allumée, il l’éteint et ajoute 1 à son compteur mental.
– Si elle éteinte, il ne fait rien.
On voit directement que chacun des prisonniers n’allumera qu’une seule fois l’ampoule, quel que soit le nombre de leur passage dans la pièce. Le Compteur lui devra à chaque fois « valider » ce passage en éteignant l’ampoule avant qu’un autre prisonnier ne puisse l’allumer, et ce 41 fois. Au final, lorsqu’il aura éteint 41 fois l’ampoule, il saura que tous les autres prisonniers sont passés au moins une fois dans la pièce et peut donc sortir de ce calvaire.
On peut remarquer que compte tenu de l’énoncé ils pourraient choisir leur Compteur comme étant le premier prisonnier à passer dans la pièce (au premier jour du début de l’expérience), un détail qui leur permettrait juste de gagner quelques jours.

OK, et combien de temps ça prendrait tout ça ?
A chaque fois que le Compteur attend avant de passer dans la pièce, la probabilité que la lampe soit allumée est la probabilité qu’un des prisonniers qui n’a pas été encore comptabilisé y aille avant lui. S’il y a k prisonniers non comptés, cette probabilité est k/(k+1). Ainsi le nombre moyen de passages avant que le Compteur voit l’ampoule allumée est de (k+1)/k.

1901 jours, un peu plus de 5 ans donc. Pas trop mal. C’est bien plus long que la méthode probabiliste, mais ça correspond à l’idée du problème qui était de trouver ce genre de stratégie.

Il existe des méthodes plus optimales, certaines utilisant des assistants au comptage, d’autres en comptant des groupes de prisonniers plutôt qu’un par un. Des méthodes qui sont bien plus complexes et plus rapide (une par exemple nous donnera des temps moyens de 532 jours, soit bien mieux que la méthode classique). Mais ce n’est pas le but de mon article de les décrire et vous invite à consulter ce document si vous voulez en savoir davantage.

Également de nombreuses variantes du problème peuvent se trouver, avec plusieurs ampoules dans la pièce, plusieurs pièces, la condition de succès qui demande cette fois que chacun des prisonniers annonce un jour correctement qu’ils sont tous passés, voire que chacun annonce le même jour (variante d’ailleurs impossible)…

Enigme : Les prisonniers et l’ampoule

Il existe de nombreuses variantes à cette énigme, celle-ci est la plus simple des versions :

42 prisonniers sont retenus dans des cellules d’isolement. Le gardien de la prison, qui a envie de s’amuser un peu, leur propose le marché suivant :
Chaque jour, il va choisir un des prisonniers, au hasard, et l’emmener dans une pièce centrale contenant une ampoule. A l’intérieur le prisonnier a la possibilité d’éteindre ou d’allumer l’ampoule via un interrupteur.
Également il a l’option de pouvoir affirmer au gardien que tous les 42 prisonniers sont passés au moins une fois dans cette pièce depuis le début de l’expérience. Si c’est le cas, le gardien les libère tous. S’il se trompe il les exécute tous. Ainsi cette affirmation ne doit se faire qu’avec une absolue certitude.
Les prisonniers se réunissent une fois seulement avant le début de l’expérience pour discuter d’un plan à adopter. Quelle doit-être leur stratégie pour s’en sortir ?

Elle présente la particularité d’avoir plusieurs solutions, certaines étant plus optimales que d’autres. Le nombre 42 est bien sûr choisi arbitrairement 🙂
La solution classique sera donnée ici. Have fun.

Le paradoxe de Banach-Tarski

Le théorème de Banach-Tarski est un paradoxe au sens où il défie l’intuition. Il affirme qu’en partant d’une boule (dans un espace à 3 dimensions) il existe une décomposition de cette boule en un nombre fini de morceaux qu’on peut rassembler pour former deux boules identiques à l’originale, à un déplacement près. La clé de ce paradoxe repose sur le fait que ces ensembles ne soient pas mesurables, ces boules n’ayant en effet pas de volume à proprement parler.

Ce site en fait une démonstration si limpide, qui bien que simplifiée couvre l’essentiel de l’idée, que je ne peux résister à vous en faire la traduction.

Vous prenez une balle, vous la découpez, et vous rassemblez les morceaux en deux balles de la même taille que la première. Cela semble fou, et à raison ! Si ce théorème marche pourtant, c’est parce qu’il s’applique à des objets mathématiques et non à des objets physiques. En particulier, il repose sur certaines propriétés des nombres réels : le fait qu’il en existe une infinité, et qu’on ne peut les associer un à un aux nombres entiers. Voyons ça de plus près.

Dans une sphère physique, une balle de tennis par exemple, il n’y a pas une infinité d’atomes, seulement un nombre fini qu’on peut séparer et réarranger. Manipuler les nombres réels donne des résultats différents. Combien y a-t-il de nombres réels entre 0 et 1 ? Une infinité. Tellement même qu’on ne pourrait les associer un à un aux nombres entiers. Combien y en a-t-il entre 0 et 2 ? Une infinité encore, mais…

Considérons une fonction qui multiplie les nombres par 2. Si l’on applique cette fonction à un nombre x entre 0 et 1, on multiplie ce nombre par 2 et le résultat y se trouve entre 0 et 2. De plus, pour chaque nombre y entre 0 et 2, il y a exactement un nombre x entre 0 et 1 qui quand on le multiplie par 2 donne y (ce nombre étant y/2).
Ainsi, les nombres réels entre 0 et 1 peuvent être associés un à un aux nombres réels entre 0 et 2 (les deux ensembles [0;1] et [0;2] sont en bijection, on dira qu’ils sont équipotents). Si dans un sens, intuitivement, il y a deux fois plus de nombres entre 0 et 2 qu’il y en a entre 0 et 1, dans un autre il y a exactement le même nombre de nombres entre 0 et 2 qu’entre 0 et 1.
Cette notion d’équipotence mériterait un article entier pour être traité plus en détail (et peut-être que j’y reviendrai), mais ça nous servira de base pour aborder, à travers les ensembles infinis de nombres, le théorème de Banach-Tarski.

On a vu qu’en appliquant une fonction comme la multiplication on pouvait associer des nombres d’un certain ensemble d’une certaine taille (ou similairement des points d’une ligne entre deux extrémités) un à un à des nombres d’un ensemble d’une autre taille. Mais la multiplication est par nature quelque chose qui étire la taille des choses. Pour démontrer le théorème de Banach-Tarski, il nous faut une association analogue qui utilise une opération qui n’étire pas les choses.
L’opération que nous allons utiliser est la rotation en trois dimensions. Si vous prenez un objet en trois dimensions et que vous le tournez, il ne s’étire pas ni ne se réduit, n’est-ce pas ?
Le reste de la démonstration va se dérouler en ignorant quelques détails. Ils devraient être traités dans une démonstration formelle, mais le but de cet article n’est pas de fournir une démonstration formelle, juste de montrer l’idée globale derrière. Allons-y !

Considérons une sphère. Pour prendre un exemple familier, disons la Terre (ne chipotons pas et oublions les anomalies et aplatissements de notre globe). Une sphère parfaite donc.
On va imaginer notre Terre en rotation autour de différents axes. Le premier qui nous vient à l’esprit est l’axe actuel de rotation qui passe par les pôles nord et sud. Il nous en faut un deuxième, à angle droit de celui-là. Prenons l’axe qui passe à travers l’équateur, passant par le méridien de Greenwich d’un côté et le 180e méridien de l’autre, tel qu’en faisant pivoter la Terre autour de cet axe les pôles nord et sud viennent tourner autour du centre.

Ok, imaginons que l’on fait tourner la Terre autour de ces axes d’un angle très précis. On peut le faire plusieurs fois, mais à chaque fois que l’on tourne la Terre, on le fait de cet angle uniquement. Cet angle que l’on choisit arbitrairement doit par contre être un nombre irrationnel de degrés, donc ça ne peut être un nombre rationnel.

On rappellera qu’un nombre rationnel est un entier divisé par un autre. Par exemple, 5/8, 2 (soit 2/1) ou -3-4/9 (soit -31/9). Un nombre rationnel peut être représenté par un nombre dont les décimales se terminent après un nombre fini de décimales, ou bien dont les décimales forment une séquence de nombres qui se répètent à l’infini (reprenant les exemples du dessus, 0.625, 2.0 et -3.444…). Un nombre irrationnel est un nombre qui ne peut pas être écrit comme un entier divisé par un autre. Représenté comme un nombre décimal, un nombre irrationnel a ses décimales qui ne s’arrêtent jamais ni ne forment une séquence répétée. Par exemple, la racine carrée de 2, le nombre π (=3.1415926…) ou le logarithme de 7 sont irrationnels.

Si l’on choisissait un nombre rationnel de degrés, soit p/q degrés, en appliquant la rotation q fois autour du même axe, on arriverait à une rotation équivalente de p degrés. Comme il y a 360° dans une rotation complète, si l’on appliquait notre rotation 360q fois, la Terre se retrouverait à l’exacte même orientation qu’au départ, et c’est quelque chose qu’on ne veut pas pour notre démonstration.
En prenant un nombre irrationnel pour l’angle de notre rotation, on se garantit que quelque soit le nombre de rotations appliquées, la Terre ne reviendra jamais à son angle initial (c’est juste une autre façon de voir la propriété comme quoi en multipliant un nombre irrationnel par un nombre entier, on n’obtient jamais un nombre entier. Étant la définition même d’un nombre irrationnel, on sait que c’est vrai). On peut se rapprocher extrêmement près de l’orientation de départ, mais jamais on y sera précisément.

La seule exception est si l’on applique des rotations inverses pour annuler les rotations initiales. Si l’on tourne 6 fois en avant, puis 6 fois en arrière, on revient au point de départ.
L’autre point intéressant est que lorsqu’on combine des rotations autour des deux axes, on ne revient jamais au point de départ non plus, quelque soit l’ordre ou le nombre de rotations effectuées. La seule exception étant encore d’appliquer la séquence inverse pour annuler la séquence initiale.

Ok, on va avoir besoin de quelques notations mathématiques maintenant. Juste un peu, rien d’effrayant.
Appelons A l’opération « tourner de l’angle choisi autour de l’axe nord-sud de la Terre dans la direction normale ». L’opération inverse « tourner de l’angle choisi autour de l’axe nord-sud de la Terre dans la direction inverse » sera A’.
La notation usuelle pour l’inverse est l’exposant -1, mais wordpress ne va pas me laisser l’utiliser facilement, alors je vais prendre le signe prime (ce qui ne devrait pas dépayser les amateurs de Rubik’s cube :p) à la place. L’opération inverse est celle qui combinée à l’opération initiale (on tourne dans une direction, puis dans l’autre du même angle) nous ramène au point de départ.
Il nous reste à nommer deux autres opérations, s’appliquant autour de l’équateur. « Tourner de l’angle choisi autour du nouvel axe dans le sens horaire en regardant l’Afrique » sera B. Et son inverse dans le sens antihoraire sera B’.

On peut ainsi écrire une suite de rotations avec ces quatre variables. On les lira de gauche à droite. Par exemple, la suite AB’A’BB veut dire :
– tourner de l’angle choisi autour de l’axe nord-sud dans le sens normal, puis
– tourner de l’angle choisi autour de l’équateur dans le sens antihoraire, puis
– tourner de l’angle choisi autour de l’axe nord-sud dans le sens inverse, puis
– tourner de l’angle choisi autour de l’équateur dans le sens horaire, puis
– tourner de l’angle choisi autour de l’équateur dans le sens horaire.

Toute suite de rotations peut ainsi s’écrire comme une suite d’une de ses quatre opérations. Un petit détail cependant, si l’on voit une opération et son inverse l’une à côté de l’autre, ses deux opérations s’annulent l’une et l’autre et on les retire de la suite. Par exemple, la suite AB’BAA’BA’ peut se simplifier en ABA’.
Avec ces notations, on peut revenir de façon plus précise sur le fait qu’on ne pourra jamais revenir à son point de départ, quelle que soit la chaîne de rotations effectuées. Les suites AAB, ABA et BAA donnent des rotations différentes de la Terre. De même, quelque chose comme ABA’ ne donne pas le même résultat que B, on ne peut pas annuler des rotations inverses s’il y a quelque chose entre (Prenez par exemple un dé à 6 faces et des rotations à 90° pour tester ce résultat).
C’est bon jusque là ?

Considérons maintenant l’ensemble de toutes les rotations possibles autour de la Terre (suivant nos contraintes). Appelons cet ensemble S. Puisqu’on ne peut tourner la Terre que de notre angle, autour de deux axes, en avant ou arrière, ça veut dire que toutes les rotations peuvent s’écrire comme une suite de A, B, A’ et B’. Comme on ne peut revenir au point de départ (l’angle étant irrationnel), une chaîne de symboles peut être aussi longue que l’on veut, et en supposant que l’on a retiré toutes les paires d’inverses qui s’annulent (simplifiant chaque chaîne à son écriture la plus courte), cette chaîne donnera toujours une nouvelle orientation unique. Il y a ainsi un nombre infini de chaînes, et un nombre infini d’orientations.
Divisons cet ensemble S entre quatre sous-ensembles :
1. L’ensemble des rotations qui commencent par A – appelons-le (ens. 1).
2. L’ensemble des rotations qui commencent par B – appelons-le (ens. 2).
3. L’ensemble des rotations qui commencent par A’ – appelons-le (ens. 3).
4. L’ensemble des rotations qui commencent par B’ – appelons-le (ens. 4).

Ça a l’air assez simple. Quelle taille ont ces ensembles ? Chacun contient un nombre infini de possibilités, ils sont donc de taille infinie. Mais il semble raisonnable de penser qu’ils ont tous la même taille. On a divisé notre ensemble S de toutes les rotations possible en quatre morceaux « égaux ».

Prenons (ens. 3), l’ensemble des rotations qui commence par A’. La première opération dans chacune de ses rotations est A’, mais ça ne nous dit rien sur ce qu’est la deuxième opération. Excepté que ça ne peut être A, parce que la rotation commencerait alors par A’A et que ça s’annulerait et serait retiré de la chaîne. Donc la deuxième opération dans chacune des rotations de (ens. 3) est B, A’ ou B’.

Tournons la Terre par l’opération A. C’est bon ? Regardons nos ensembles de rotations. Toutes les rotations sont les mêmes, avec un A placé devant.
Examinons (ens. 3) encore. Toutes les rotations de (ens. 3) sont les mêmes qu’avant, mais avec un A placé devant. Mais les rotations de (ens. 3) commençaient toutes par A’. Ainsi elles commencent toutes désormais par AA’. Ces deux opération s’annulent et on peut les retirer. Ce faisant, la première opération d’une rotation de (ens. 3) est maintenant l’ancienne deuxième opération. Mais cette deuxième opération des rotations de (ens. 3) est soit B, A’ ou B’. Donc (ens. 3), après avoir tourné la Terre par A, comprend toutes les rotations des ensembles 2, 3 et 4 !

En d’autres mots, par une simple rotation de la Terre par A, on a transformé l’ensemble des rotations (ens. 3) en l’ensemble des rotations (ens. 2) plus (ens. 3) plus (ens. 4).
Arrêtons nous pour réfléchir à ce que ça veut dire pour chacune des rotations possibles, l’ensemble S.
On a commencé en divisant S en quatre morceaux, (ens. 1), (ens. 2), (ens. 3) et (ens. 4). Ainsi on peut dire :
S =  (ens. 1) + (ens. 2) + (ens. 3) + (ens. 4)

Jusque là ça va. Mais on vient juste de voir qu’en tournant la Terre par A, on transformait (ens. 3) en (ens. 2) plus (ens. 3) plus (ens. 4). Ainsi on peut écrire :
S = (ens. 1) + (ens. 3 après avoir tourné la Terre par A)
On n’a plus besoin de (ens. 2) ou de (ens. 4) ! Aussi, de façon similaire, en tournant la Terre par B à la place de A, on transformerait (ens. 4) en (ens. 1) plus (ens. 3) plus (ens. 4), et ainsi écrire :
S = (ens.2) + (ens. 4 après avoir tourné la Terre par B)

Au final, qu’est-ce qu’on a montré ? Que si on prenait l’ensemble S de toutes les rotations possibles autour de la Terre (suivant nos contraintes), on pouvait les diviser en quatre sous-ensembles. Par une rotation de l’un de ses ensembles par A, et d’un autre par B, on peut combiner deux de ces ensembles pour générer S, et on peut combiner les deux autres pour générer une autre copie complète de S.

Très bien, mais on parle juste d’ensemble de rotations, pas de parties réelles de la Terre. Mais on a fait le plus gros du travail. Considérons maintenant des points à la surface de la Terre. Par « point » ce n’est pas des endroits comme « Paris » ou « la Tour Eiffel », mais des points mathématiques comme 34.432913…° N, 127.348762…° W. Chaque latitude et longitude distinctes forment donc un point, et la latitude et la longitude peuvent être tout nombre réel dans leur écart respectif de valeurs (et avoir un nombre infini de décimales).

Prenons un point à la surface de la Terre, peu importe où. Quand on applique à ce point la rotation A (tournant juste ce point autour du centre de la Terre cette fois, et pas la Terre toute entière), on se retrouve avec un nouveau point à la surface de la Terre. De même si l’on tourne par B, A’, ou AB’A’BB, ou n’importe quelle autre rotation de notre ensemble S. Imaginons tous les points possibles à la surface de la Terre que l’on peut atteindre en appliquant toutes les rotations possibles de S à notre point de départ. C’est un ensemble infini de points, répartis très densément sur toute la surface de la Terre (dans chaque millimètre carré de la Terre, il y aura une infinité de ces points).

Mais ce n’est pas nécessairement tous les points de la Terre. Il y a également une infinité de points que l’on ne peut pas atteindre partant de notre point de départ et en appliquant n’importe quelle rotation de S. Prenons donc un autre point parmi ceux-là. Et imaginons l’ensemble de tous les points que l’on peut atteindre partant de ce point-ci en lui appliquant les rotations de S. C’est un autre ensemble de points à la surface de la Terre. Vous l’aurez deviné, il y a encore des points non atteints. Prenons-en un autre et appliquons-lui S…

Il faudrait ainsi prendre une infinité de points de départ pour être sûr d’atteindre tous les points à la surface de la Terre en utilisant les rotations de S. Mais ce n’est pas un problème. En fait, on a coupé la surface de la Terre en une infinité d’ensemble de points, chaque « tranche » étant composée de points dont on peut se déplacer de l’un à l’autre par une rotation de S ; et il est impossible de se déplacer d’un point d’une tranche vers un point d’une autre tranche par une rotation de S.

Allons plus loin. Créons un nouvel ensemble de points, appelons le M. Cet ensemble M sera composé d’exactement un point de chaque tranche précédemment définie. Peu importe quel point on choisit, tant que l’on en prend un et un seul dans chaque tranche. Si l’on peut faire cela, c’est grâce à l’axiome du choix.

Petit aparté sur l’axiome du choix. Un axiome est en mathématiques une vérité première, une propriété indémontrable qui sert de base à un système de logique. L’axiome du choix s’énonce ainsi : « Étant donnée une famille non vide d’ensembles non vides, il existe une fonction, appelée fonction de choix qui à chacun d’entre eux associe un de ses éléments. ». Cet axiome est assez controversé, et optionnel, notamment parce que s’il affirme l’existence d’un objet, il ne donne aucune façon de le trouver. C’est pourquoi, même si la plupart des mathématiciens l’utilisent sans réticence, d’autres éviteront d’y avoir recours quand ils le peuvent. Cet axiome sert particulièrement lorsqu’il faut faire un choix dans un ensemble infini (il n’est pas nécessaire dans un ensemble fini), ce qui est le cas pour le théorème de Banach-Tarski.

Bref l’axiome du choix nous permet de créer cet ensemble M qui va se révéler très intéressant.
Pensez à n’importe quel point à la surface de la Terre. Il y a exactement un point dans l’ensemble M à partir duquel on peut appliquer une rotation de S pour obtenir votre point. C’est vrai parce que c’est ainsi que l’on a défini M. Ainsi, on peut atteindre n’importe quel point à la surface de la Terre en commençant d’un point précis de M et en lui appliquant une rotation particulière de S, et on ne peut l’atteindre en commençant d’un autre point ou en utilisant une autre rotation.

Maintenant, divisons la surface de la Terre en quatre parties :
1. La partie des points que l’on peut atteindre commençant d’un point de M et utilisant uniquement une rotation de (ens. 1). Appelons-la (partie 1).
2. La partie des points que l’on peut atteindre commençant d’un point de M et utilisant uniquement une rotation de (ens. 2). Appelons-la (partie 2).
3. La partie des points que l’on peut atteindre commençant d’un point de M et utilisant uniquement une rotation de (ens. 3). Appelons-la (partie 3).
4. La partie des points que l’on peut atteindre commençant d’un point de M et utilisant uniquement une rotation de (ens. 4). Appelons-la (partie 4).

La surface de la Terre est la somme de ces quatre parties :
Surface de la Terre = (partie 1) + (partie 2) + (partie 3) + (partie 4)

Mais que se passerait-il si l’on tournait la Terre par A ? L’ensemble des rotations (ens. 3) devient égal à (ens. 2) + (ens. 3) + (ens. 4), comme on l’a montré plus haut. Donc (partie 3) devient égal à (partie 2) + (partie 3) + (partie 4). Et on a :
Surface de la Terre = (partie 1) + (partie 3 après avoir tourné la Terre par A)

De même, en tournant par B on obtient :
Surface de la Terre = (partie 2) + (partie 4 après avoir tourné la Terre par B)

Donc on a coupé la surface de la Terre en quatre parties. Si l’on tourne l’une de ces parties d’une certaine façon, on peut la combiner avec une autre de ces parties pour obtenir la surface totale de la Terre. Et avec les deux parties restantes, en tournant l’une d’elles d’une certaine façon, on peut les combiner pour obtenir une autre copie complète de la surface de la Terre.
On se rapproche de la fin là ! Il nous reste à étendre cela au volume de la Terre, ce qui est relativement simple. Pour chaque partie de la surface de la Terre, prenons le volume de la Terre égal à cette partie plus tout l’espace sous les points de cette partie jusqu’au centre de la Terre. On a ainsi quatre volumes :
1. Le volume de la Terre de et sous (partie 1). Appelons-le (volume 1).
2. Le volume de la Terre de et sous (partie 2). Appelons-le (volume 2).
3. Le volume de la Terre de et sous (partie 3). Appelons-le (volume 3).
4. Le volume de la Terre de et sous (partie 4). Appelons-le (volume 4).

On peut diviser la Terre en ces quatre volumes :
Terre = (volume 1) + (volume 2) + (volume 3) + (volume 4)

Et vous l’aurez deviné :
Terre = (volume 1) + (volume 3 après avoir tourné la Terre par A)
et :
Terre = (volume 2) + (volume 4 après avoir tourné la Terre par B)
Ta da !

Il resterait quelques détails à traiter. Avec ces notations on a vu que l’on pouvait diviser une sphère en quatre parties et les rassembler en deux sphères de même taille. Le théorème de Banach-Tarski montre qu’il en faut en fait cinq. En effet la partie supplémentaire contient tous les points « mis de côtés ». Ces points comportent le centre de la sphère (qui ne peut être inclus dans aucun des volumes définis plus haut), les points des axes de rotations (qui ne bougent pas quand on leur applique la rotation de leur axe). Y sont également les points de l’ensemble M lui-même, qu’on ne peut atteindre en partant d’un point de M et en appliquant une rotation (la rotation qu’on aurait besoin d’appliquer est la rotation « nulle » consistant en une chaîne de zéro A, B, A’, B’. Bien que ça soit une opération valide, elle n’est pas incluse dans l’ensemble des rotations commençant par chacun de ces symboles, puisqu’elle n’a aucun symbole). Ces détails ne ruinent pas la démonstration du théorème, juste qu’il faudrait les traiter pour une explication plus complète.

Bon, vous êtes soit émerveillés d’avoir tout compris, ou vous êtes perdus quelque part entre ces lignes (je m’en excuse alors), ou bien vous vous dites qu’il doit y avoir quelque chose de faux quelque part, parce que c’est impossible que ça soit vrai.

Il est important de redire que c’est un résultat mathématique, qui ne s’applique qu’à des sphères en trois dimensions, infiniment divisibles. On ne peut pas l’appliquer à la Terre (en excluant le côté pratique), parce que la Terre est composée d’un nombre discret (fini) d’atomes. Les parties et volumes décrites plus haut ne sont pas de simples objets facilement visualisables, ils sont constitués d’ensembles dispersés d’un nombre infini de points. Ce serait plus un motif fractal qu’une orange.

Une des choses que nous dit le théorème de Banach-Tarski est que le concept de volume d’un objet mathématique à trois dimensions n’est pas aussi facilement défini que l’intuition laisserait paraître. C’est même un problème bien connu en mathématiques, il est extrêmement difficile de définir le volume d’un objet mathématique de façon à ce qu’il correspond au volume tel qu’on le connait. Les amateurs de théorie de la mesure savent ce qu’il en est.

Je le redis aussi, ici n’est montrée qu’une démonstration simplifiée et les détails les plus délicats ont été laissés de côté, mais ça ne change pas le résultat du théorème de Banach-Tarski.

Merci encore à David Morgan-Mar pour son explication si claire.

Enigme : Le roi envolé [Solution]

Court énoncé mais solution tordue ! Voici la solution à notre énigme :

Il convient d’abord de se demander à qui était le trait. Si c’était aux blancs de jouer, ils pourraient prendre le roi noir, ce qui est impossible, à moins que le roi blanc ne se trouve en b3. Mais si c’était le cas, il n’y a aucun coup noir qui permette ce double échec par la tour+fou.

Les blancs viennent donc de jouer. Ils n’ont pas pu bouger leur fou car ils auraient pu prendre le roi noir alors. Ils ont donc déplacé le roi blanc, et de même à cause du fou ce roi se trouvait avant en b3.

Le roi blanc était en b3 donc, en échec double, et n’a que deux cases où se déplacer : a3 et c3.

Reste à trouver ce qui a permis cet échec double. La seule possibilité se trouve via un échec à la découverte, mais la disposition empêche le fou de découvrir la tour, ou inversement. C’est donc qu’il y avait une autre pièce noire sur l’échiquier, prise par le roi dans son déplacement.

C’est là que vient l’astuce. Cette pièce noir devait se trouver en b4 ou c4 (pour découvrir la tour ou le fou), mais si le roi blanc la prend c’est qu’elle se déplace en a3 ou c3. Or il faut une autre pièce en c4/b4, que celle en b4/c4 va prendre pour permettre l’échec double. Prendre une pièce tout en se déplaçant vers une autre case ? La seule solution est la prise en passant !
On a ainsi cette disposition. Le dernier coup a été le fou noir, venant de n’importe où sur la diagonale et mettant le roi blanc en échec. c2-c4 du pion blanc, prise en passant du noir b4xc3, le roi blanc le prend en c3, puis est balayé par le coup de vent, fin de l’énigme !

Enigme : Le roi envolé

Une petite énigme d’échecs pour changer.

Évidemment elle suppose que vous connaissiez les règles de ce jeu pour la résoudre. Enjoy :

Au cours d’une partie, le roi blanc a été soufflé par un coup de vent et est tombé de l’échiquier. Par chance les autres pièces n’ont pas bougé. Où se trouvait-il avant de disparaître ?

La solution de cette énigme se trouvera ici.

Enigme : Le butin des pirates [Solution]

Voici donc la solution à notre énigme.

Classons déjà nos 5 pirates par degré de férocité. Le moins sauvage étant P1, allant jusqu’à P5 le plus dangereux.
De façon similaire à l’énigme des yeux, pour la résoudre il convient de partir à l’envers depuis un cas simplifié et de remonter jusqu’à la solution globale. Chaque décision de pirate dépendant de ce que feraient les suivants, il ne serait pas pratique de commencer par le début.

Regardons ce qui se passe s’il ne reste que deux pirates. Le cas extrême où il ne reste qu’un seul pirate est trivial vu qu’il repart avec tout l’or, mais il est surtout impossible à atteindre car avec deux pirates restants, P1 et P2, P2 propose son partage, 100 pour lui et 0 pour P1, P2 vote pour lui-même et avec sa seule voix obtient 50% des votes et la proposition est acceptée.

Rajoutons maintenant le pirate P3. Chacun sait que si la proposition de P3 est refusée, on se retrouve à deux pirates et P1 n’aura rien. P3 sait donc que P1 acceptera toute proposition qui lui rapporterait mieux que rien. P3 a donc à donner 1 pièce à P3 et 99 pour lui-même. De cette façon il s’assure du vote de P1, plus le sien, ce qui lui donne la majorité.

Avec P4 c’est le même raisonnement. P4 sait que P2 n’aura rien si son vote est refusé . Il propose 1 pièce à P2 et 99 pour lui-même. P2 votera pour lui, ce qui fera 50% des voix avec la sienne.

P5 doit agir de la même façon, mais il doit par contre soudoyer deux pirates. Il sait que P1 et P3 n’auront rien si P4 se retrouvait à décider d’un partage. Il lui suffit donc de leur proposer 1 pièce à chacun pour s’assurer de leur vote. Le partage final est donc 98 pour P5, 0 pour P4, 1 pour P3, 0 pour P2 et 1 pour P1.

Passons aux choses sérieuses, avec 500 pirates !
On a toujours 100 pièces d’or à partager. Il est clair que le même motif de partage se retrouve jusqu’à un certain nombre. Avec 10 pirates, on aurait 0-1-0-1-0-1-0-1-0-96. On voit que lorsque le nombre de pirates est pair (n=2k pirates), tous les pirates impairs se retrouvent avec rien, les pirates pairs reçoivent 1 sauf le dernier (celui qui partage) qui reçoit 100-(k-1) pièces d’or. Pour un nombre impair de pirates (n=2k+1), les pirates pairs ne reçoivent rien, les pirates impairs reçoivent une pièce sauf le dernier qui reçoit 100-k pièces d’or.

Cela n’est vrai que jusqu’au 200e pirate. P200 n’offre rien aux pirates impairs de P1 à P199, et une pièce d’or aux pirates pairs de P2 à P198, ce qui lui laisse une seule pièce pour lui-même.

Ensuite ça devient intéressant ! P201 n’a que 100 pièces à partager et ne peut espérer repartir avec une pièce. Mais il a tout de même un intérêt à ne pas être jeter par-dessus bord. Il propose ainsi 1 pièce à chaque pirate impair de P1 à P199 et rien pour lui-même.

Le pirate P202 est forcé d’agir pareil. Il utilise les 100 pièces d’or pour soudoyer 100 pirates. Ces 100 doivent être ceux qui n’auraient rien sous la proposition de P201. On remarque que comme il y a 101 pirates qui n’auraient rien avec P201, la distribution n’est plus unique et on a ainsi 101 façons de répartir 100 pièces d’or parmi eux.
On a donc 101 pirates qui pourraient avoir quelque chose par la proposition de P202, et 101 pirates qui sont sûrs de ne rien avoir.

Le pirate P203 doit obtenir 102 votes pour une majorité (soit 101 pirates + lui-même, et il n’a pas assez d’or pour soudoyer 101 de ses camarades. Donc P203 est condamné à la planche (si on arrive jusqu’à lui). Mais ça ne veut pas dire qu’il ne participe plus au raisonnement.

P204 sait que P203 sera jeté par-dessus bord si les votes arrivaient jusqu’à lui. Il sait donc que P203 votera pour n’importe laquelle de ses proposition juste pour éviter la planche.  Il faut 102 votes à P204 pour obtenir la majorité, il peut compter sur le vote de P203, le sien et de 100 autres pirates qu’il peut soudoyer avec les 100 pièces. Ces 100 pirates sont parmi les 101 pirates qui n’auraient rien par la proposition de P202.

A P205 maintenant. Pas de bol pour lui, il lui faut 103 votes pour survivre, mais il ne peut compter sur ceux de P204 et P203 qui se feront le plaisir de le jeter par-dessus bord (sans rien gagner de plus après !). P205 est donc tué quoi qu’il arrive.

De même pour P206, s’il est sûr d’avoir le vote de P205, ça ne suffit pas.
Pareil pour P207 qui a besoin de 104 votes. Il a déjà le sien, plus ceux de P205 et P206, et de 100 pirates soudoyés. Mais ça ne suffit pas.

Ça change pour P208. Il lui faut également 104 votes, mais il aura P205 P206 et P207 qui voteront pour lui. En ajoutant les 100 pirates à qui il offre une pièce. Il obtient ses 104 votes et survit. Ces 100 pirates soudoyés doivent se trouver parmi ceux qui n’auraient rien sous la proposition de P204 : Les pirates pairs de P2 à P200, P201, P202, P203 et P204.

On commence à voir le motif. Les pirates qui peuvent s’en sortir (toujours en ne se donnant rien et offrant les pièces à 100 pirates) s’alternent avec des suites de plus en plus longues de pirates qui seront jetés par-dessus bord de toute façon, et qui voteront ainsi pour les premiers pour sauver leur peau. Les pirates qui s’en sortiraient sont P201, P202, P204, P208, P216, P232, P264, P328, et P456 (si on arrête à 500), soit les pirates dont le nombre est 200 plus une puissance de 2.
Il reste à répartir les 100 pièces d’or, juste en s’assurant qu’elles seront reçues par des pirates qui les accepteront. La solution n’est pas unique, mais une façon de le faire est que P201 offre à tous les pirates impairs de P1 à P199, que P202 offre à tous les pirates pairs de P2 à P200, que P204 offre à tous les pirates impairs, etc.
Le résultat final est donc, pour 500 pirates : Les 44 premiers pirates sont jetés par-dessus bord. P456 offre une pièce à tous les pirates impairs de P1 à P199, et les autres sont juste contents de sortir vivants de tout ce bordel. Grâce à ce brillant système démocratique, les pirates s’arrangent pour se débarrasser des plus dangereux, et ce sont les plus calmes qui ont une chance d’avoir quelque chose.

Enigme : Le butin des pirates

Une autre, une autre !
Deux questions ici, une facile et une plus complexe. Voici l’énigme des pirates :

Un groupe de 5 pirates cherche à se partager un butin de 100 pièces d’or.
Fonctionnant sous une démocratie particulière, le plus féroce d’entre eux propose un partage, une répartition des pièces d’or entre eux (« moi j’ai x pièces, lui a y pièces, lui a z pièces, etc. »), et chacun d’eux (y compris celui qui l’a proposé) vote pour ou contre ce partage. Si la proposition obtient 50% ou plus des voix, elle est acceptée, sinon elle est rejetée et le pirate qui l’a proposée est jeté par-dessus bord. Dans ce cas c’est le pirate suivant (toujours classé par degré de férocité !) qui propose un partage aux restants.
Tous les pirates adorent jeter leurs compagnons par-dessus bord, mais s’ils ont le choix ils préfèrent obtenir de l’or. Chaque pièce est indivisible, et les arrangements pour partager des pièces après coup ne sont pas permis parce que les pirates ne se font pas confiance. Les pirates n’aiment pas être tués (étonnant !). Ils sont tous rationnels et raisonnent donc uniquement de façon logique (vraiment étonnant là !).
Enfin tous les pirates connaissent l’ensemble de ces règles.

– Le pirate le plus féroce propose son partage. Quelle est la somme qu’il peut espérer obtenir ?
– Même question, mais avec 500 pirates, et toujours 100 pièces d’or.

La solution à cette énigme se trouvera ici.

Le paradoxe de Newcomb

Le paradoxe de Newcomb, nommé son créateur le physicien William Newcomb, est plus une expérience de pensée de la théorie de la décision sur le libre-arbitre et la causalité qu’un simple problème mathématique de théorie des jeux.

Il se présente ainsi :

On vous propose de choisir parmi deux boîtes, A et B. On vous laisse soit prendre la boîte B, soit repartir avec les deux boîtes A et B.
La boîte A contient 1 000 €, la boîte B contient 1 000 000 € ou 0 € selon une condition particulière.
En effet la veille de votre choix, un devin fait une prédiction infaillible et remplit la boîte B en fonction :
– S’il prédit que vous ne prenez que la boîte B, il y met 1 000 000 €.
– S’il prédit que vous allez prendre les deux, il n’y met rien.
Que choisissez-vous ?

A ce problème, publié et analysé par le philosophe Robert Nozick en 01969, deux solutions tout autant justifiées apparaissent.
– Solution 1 : Vous prenez les deux boîtes, car au moment où vous prenez votre décision la boîte B a déjà son contenu. Dans tous les cas, vous aurez 1 000 € de plus en rajoutant la boîte A.
– Solution 2 : Choisir la boîte B garantit 1 000 000 €. En prenant les deux, le devin l’ayant prédit, on ne repart qu’avec 1 000 €.

Alors, que faire ?
Si on étudie le problème d’une approche mathématique, par le principe de dominance choisir les deux boîtes rapportant plus dans tous les cas, il convient de choisir les deux. Quelque soit le contenu de la boîte B, on obtient 1 000 € de plus en prenant les deux.
Mais l’énoncé indique le devin fait une prédiction toujours correcte. On peut ainsi mettre de côté les cas où la prédiction est fausse. Le choix est donc entre gagner 1 000 000 € en prenant juste B ou gagner 1 000 € en prenant les deux.
En supposant maintenant que le prédiction n’est que « presque toujours » correcte, par exemple à 99%, on peut calculer l’espérance de gain par choix :
– En choisissant les deux boîtes, on gagne en moyenne 1 000 € * 0.99 + 1 000 100 € * 0.01 = 11 000 €
– En choisissant la boîte B, on gagne en moyenne 0.99 * 1 000 000 € + 0.01 * 0 € = 990 000 €.
Et la décision en voulant maximiser l’espérance de gain serait donc de ne prendre que la boîte B.

La question partage, et chaque camp  semble convaincu de la pertinence de son choix. Newcomb d’ailleurs recommandait de ne prendre qu’une boîte alors que Nozick y choisissait les deux.

Ma « solution » du problème :
Est-ce au moins un paradoxe ? Ça le serait si les deux arguments étaient aussi forts de telle sorte qu’on ne puisse jamais aboutir à une résolution. En tenant compte de l’énoncé, et en supposant raisonnable le fait que le devin puisse prédire correctement, l’argument de choisir une seule boîte m’apparaît comme évident.
Certes il fait intervenir des éléments surnaturels comme l’existence d’un être omniscient reniant notre libre-arbitre, mais ce problème n’est qu’une expérience théorique utilisant des hypothèses impossibles et n’a pas but d’être analysé de façon réaliste.
Remplaçons l’idée d’une prédiction par une machine à voyager dans le temps. Le devin voit votre choix et retourne dans le passé pour y mettre le contenu des boîtes. Il apparaît clairement que le devin ne se trompera jamais et qu’il faut prendre uniquement la boîte B dans ce cas. Le paradoxe n’existe que si les gens lisent l’énoncé et ne tiennent pas compte de ce qui y est indiqué.

Enigme : Les trois princesses [Solution]

Voyons la solution de cette énigme.
A première vue on pourrait la croire impossible. En effet, comment avec une seule question, dont on ne peut avoir que deux réponses possibles, pourrait-on départager trois personnes ?
Il s’agit en fait de bien comprendre l’énoncé. Car s’il y a bien trois princesses, le but n’est pas de déterminer qui est qui parmi les trois. Ce que l’on cherche, c’est partir avec la plus âgée ou la plus jeune. Il y a donc deux issues : soit on tombe sur celle qu’on veut (aînée ou benjamine), soit sur la mauvaise (cadette).
On doit donc trouver une question à laquelle l’aînée et la benjamine répondraient la même chose, et la cadette autre chose. Sachant que cette dernière répond au hasard… ça reste compliqué !

Si l’on ne peut différencier physiquement les trois sœurs, on peut par contre les classer. L’âge est une bonne relation d’ordre, tout comme le degré de vérité (l’énoncé n’avait en effet pas besoin de différencier les princesses par leurs âges et le problème aurait été le même s’il nous avait été présenté trois triplées d’âge égal). Ainsi ici « être plus âgé que » est équivalent à « dire plus la vérité que ».

Appelons nos trois princesses A B et C, sans savoir qui est qui bien sûr.
Posons à A la question suivante : « Est-ce que B est plus âgée que C ? »
Regardons les différentes possibilités :
– Si A est l’aînée (= dit la vérité) et que B est la cadette (= ment aléatoirement), A répondra oui.
– Si A est l’aînée et que B est la benjamine (= ment toujours), A répondra non.
Ainsi si A est l’aînée, il faudrait choisir C quand A dit oui, et B quand A dit non.
– Si A est la benjamine et que B est l’aînée, A répondra non (B est plus âgée que C mais A ment).
– Si A est la benjamine est que B est la cadette, A répondra oui.
Ainsi si A est la benjamine, il faudrait choisir B quand A dit non, et C quand A dit oui.
On remarque que ce sont les mêmes actions que A soit la plus âgée ou la plus jeune.

Mais si A est la cadette alors ?
– Si A est la cadette, sa réponse est aléatoire. Que vous choisissez B ou C, de toute façon vous tomberez sur la « bonne » princesse.
C’est là toute la subtilité de l’énigme. Vous ne cherchez pas à déterminer quelle est la princesse que vous choisissez, vous vous assurez juste qu’elle ne soit pas une qui mente de temps en temps (comme quelqu’un de normal en fait !).
Ainsi si A est la cadette, il faudrait choisir B ou C.

Bilan, en prenant B quand la réponse est non et C quand la réponse est oui, vous êtes sûr de ne pas tomber sur la mauvaise. Pfiou !